ЧЕМ ОТЛИЧАЮТСЯ ЧИСЛА СО ЗНАКОМ И БЕЗ ЗНАКА
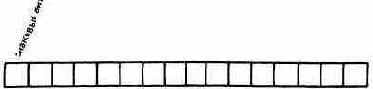
Все цифровые компьютеры хранят числа в двоичной форме1. Элемент стека Форт-системы состоит из 16 разрядов2, или битов (бит - двоичная цифра). Ниже показана структура из 16 битов, где приводятся значения всех битов:

Если в каждом бите хранится единица, то это число составит 65535. Таким образом, 16 битами можно представить любое значение от 0 до 65535. Поскольку такой способ представления не позволяет нам изображать отрицательные числа, мы называем их числами без знака. В наших таблицах и стековой нотации числа без знака обозначаются буквой и.
1 Для тех, кто не знаком с двоичной системой счисления. Попросите кого-нибудь из ваших друзей (увлекающегося математикой) рассказать вам об этой системе или поищите учебное пособие по ЭВМ для начинающих.
2 Для пользователей 32-разрядных компьютеров. В таких процессорах, как 68000, стек Форта обычно 32-разрядный. Поэтому термин, число одинарной длины в данном случае означает 32-разрядное число.
Но как же быть с отрицательными числами? Чтобы иметь возможность изображать как положительные, так и отрицательные числа, необходимо пожертвовать одним битом, задействовав его под знак. Для этой цели мы отведем самый левый «старший по порядку» бит. 15 оставшихся бит позволят нам представить любое число вплоть до 32767. Если знаковый бит содержит единицу, то нужно отложить изображаемое значение по оси влево от нуля, т. е. в области отрицательных чисел. Таким образом, с помощью 16 бит можно представить число в диапазоне от -32768 до +32767. Вы уже знаете, что этот диапазон составляют числа одинарной длины, обозначаемые буквой п.
Мы столь подробно останавливаемся на представлении отрицательных чисел, чтобы у вас была полная ясность по всем излагаемым здесь вопросам. У вас может сложиться впечатление, что достаточно просто ввести знаковый разряд, и вы сможете различить отрицательное и положительное числа, однако на самом деле это далеко не так.
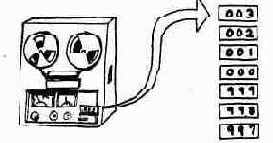
Чтобы понять, как представляются отрицательные числа, вернемся снова к десятичной системе счисления и понаблюдаем за показаниями счетчика, устанавливаемого на магнитофонах многих типов.
Допустим, что счетчик высвечивает три цифры (трехзначное число). По мере перемотки ленты это число увеличивается. Установим счетчик на нуль и начнем перематывать ленту в обратном направлении. Первое число, которое вы увидите на индикаторе, будет 999. Его мы воспринимаем как - 1. Следующим числом окажется 998, что соответствует -2, и т. д.
Аналогично представляются числа со знаком и в компьютере. Если мы начнем с нуля:
0000000000000000
и вернемся назад на одно число, то будем иметь
1111111111111111 (16 единиц)
что означает 65535 при изображении чисел без знака и -1 при изображении чисел со знаком. Число 1111111111111110
соответствует 65534 при изображении чисел без знака и -2 при изображении чисел со знаком.
(Традиционно числа -1 и 0 применяются в качестве значений «истина» и «ложь» потому, что в представлении -1 все биты установлены, а в представлении 0 - сброшены.)
Ниже приводится схема, в которой показано, каким образом двоичное число в стеке может использоваться как число без знака или как число со знаком.
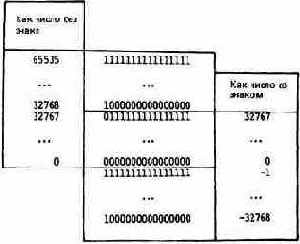
Такой странный на первый взгляд способ представления отрицательных чисел дает возможность компьютеру использовать одни и те же процедуры для выполнения как вычитания, так и сложения.
Продемонстрируем изложенное на примере простой задачи: 2 - 1 ---
Эта задача эквивалентна задаче сложения 2+ (-1). При двоичном представлении чисел одинарной длины двойка выглядит следующим образом:
0000000000000010
а отрицательная единица - так:
1111111111111111
Компьютер складывает их таким же образом, как мы это делаем на бумаге. Если сумма в какой-то колонке превышает единицу, то в следующую колонку (старший двоичный разряд) переносится 1. В результате получается: 0000000000000010 + 1111111111111111 ----------------- 1000000000000001
Как видите, компьютеру потребовалось выполнить перенос единицы в старший разряд во всех колонках, а последняя единица была вынесена в 17-й разряд. Но так как элемент стека состоит только из 16 битов, будет выведено число 0000000000000001 т.е. единица, что является правильным ответом.
Мы не объясняем здесь, каким образом компьютер переводит положительное число в отрицательное. При желании вы можете найти описание этого процесса, который называется «дополнением до двух», в литературе.
