Байесовская фильтрация по словам
Не так давно баесовская классификация была предложена для персональной фильтрации спама. Первый фильтр был разработан Полем Грахемом (Paul Graham). Для работы алгоритма требуется выполнение двух требований.
Первое требование - необходимо, чтобы у классифицируемого объекта присутствовало достаточное количество признаков. Этому идеально удовлетворяют все слова писем пользователя, за исключением совсем коротких и очень редко встречающихся.
Второе требование - постоянное переобучение и пополнение набора "спам - не спам". Такие условия очень хорошо работают в локальных почтовых клиентах, так как поток "не спама" у конечного клиента достаточно постоянен, а если изменяется, то не быстро.
Однако для всех клиентов сервера точно определить поток "не спама" довольно сложно, поскольку одно и то же письмо, являющееся для одного клиента спамом, для другого спамом не является. Словарь получается слишком большим, не существует четкого разделения на спам и "не спам", в результате качество классификации, в данном случае решение задачи фильтрации писем, значительно снижается.

Байесовская классификация
Альтернативные названия: байесовское моделирование, байесовская статистика, метод байесовских сетей.
Ознакомиться детально с байесовской классификацией можно в [11]. Изначально байесовская классификация использовалась для формализации знаний экспертов в экспертных системах [40], сейчас баесовская классификация также применяется в качестве одного из методов Data Mining.
Так называемая наивная классификация или наивно-байесовский подход (naive-bayes approach) [43] является наиболее простым вариантом метода, использующего байесовские сети. При этом подходе решаются задачи классификации, результатом работы метода являются так называемые "прозрачные" модели.
"Наивная" классификация - достаточно прозрачный и понятный метод классификации. "Наивной" она называется потому, что исходит из предположения о взаимной независимости признаков.
Свойства наивной классификации:
Использование всех переменных и определение всех зависимостей между ними.Наличие двух предположений относительно переменных: все переменные являются одинаково важными;все переменные являются статистически независимыми, т.е. значение одной переменной ничего не говорит о значении другой.Большинство других методов классификации предполагают, что перед началом классификации вероятность того, что объект принадлежит тому или иному классу, одинакова; но это не всегда верно.
Допустим, известно, что определенный процент данных принадлежит конкретному классу. Возникает вопрос, можем ли мы использовать эту информацию при построении модели классификации? Существует множество реальных примеров использования этих априорных знаний, помогающих классифицировать объекты. Типичный пример из медицинской практики. Если доктор отправляет результаты анализов пациента на дополнительное исследование, он относит пациента к какому-то определенному классу. Каким образом можно применить эту информацию? Мы можем использовать ее в качестве дополнительных данных при построении классификационной модели.
Отмечают такие достоинства байесовских сетей как метода Data Mining [41]:
в модели определяются зависимости между всеми переменными, это позволяет легко обрабатывать ситуации, в которых значения некоторых переменных неизвестны;байесовские сети достаточно просто интерпретируются и позволяют на этапе прогностического моделирования легко проводить анализ по сценарию "что, если";байесовский метод позволяет естественным образом совмещать закономерности, выведенные из данных, и, например, экспертные знания, полученные в явном виде;использование байесовских сетей позволяет избежать проблемы переучивания (overfitting), то есть избыточного усложнения модели, что является слабой стороной многих методов (например, деревьев решений и нейронных сетей).Наивно-байесовский подход имеет следующие недостатки:
перемножать условные вероятности корректно только тогда, когда все входные переменные действительно статистически независимы; хотя часто данный метод показывает достаточно хорошие результаты при несоблюдении условия статистической независимости, но теоретически такая ситуация должна обрабатываться более сложными методами, основанными на обучении байесовских сетей [42];невозможна непосредственная обработка непрерывных переменных - требуется их преобразование к интервальной шкале, чтобы атрибуты были дискретными; однако такие преобразования иногда могут приводить к потере значимых закономерностей [43];на результат классификации в наивно-байесовском подходе влияют только индивидуальные значения входных переменных, комбинированное влияние пар или троек значений разных атрибутов здесь не учитывается [43]. Это могло бы улучшить качество классификационной модели с точки зрения ее прогнозирующей точности, однако,увеличило бы количество проверяемых вариантов. Байесовская классификация нашла широкое применение на практике.
Линейный SVM
Решение задачи бинарной классификации при помощи метода опорных векторов заключается в поиске некоторой линейной функции, которая правильно разделяет набор данных на два класса. Рассмотрим задачу классификации, где число классов равно двум.
Задачу можно сформулировать как поиск функции f(x), принимающей значения меньше нуля для векторов одного класса и больше нуля - для векторов другого класса. В качестве исходных данных для решения поставленной задачи, т.е. поиска классифицирующей функции f(x), дан тренировочный набор векторов пространства, для которых известна их принадлежность к одному из классов. Семейство классифицирующих функций можно описать через функцию f(x). Гиперплоскость определена вектором а и значением b, т.е. f(x)=ax+b. Решение данной задачи проиллюстрировано на рис. 10.4.
В результате решения задачи, т.е. построения SVM-модели, найдена функция, принимающая значения меньше нуля для векторов одного класса и больше нуля - для векторов другого класса. Для каждого нового объекта отрицательное или положительное значение определяет принадлежность объекта к одному из классов.

Рис. 10.4. Линейный SVM
Наилучшей функцией классификации является функция, для которой ожидаемый риск минимален. Понятие ожидаемого риска в данном случае означает ожидаемый уровень ошибки классификации.
Напрямую оценить ожидаемый уровень ошибки построенной модели невозможно, это можно сделать при помощи понятия эмпирического риска. Однако следует учитывать, что минимизация последнего не всегда приводит к минимизации ожидаемого риска. Это обстоятельство следует помнить при работе с относительно небольшими наборами тренировочных данных.
Эмпирический риск - уровень ошибки классификации на тренировочном наборе.
Таким образом, в результате решения задачи методом опорных векторов для линейно разделяемых данных мы получаем функцию классификации, которая минимизирует верхнюю оценку ожидаемого риска.
Одной из проблем, связанных с решением задач классификации рассматриваемым методом, является то обстоятельство, что не всегда можно легко найти линейную границу между двумя классами.
В таких случаях один из вариантов - увеличение размерности, т.е. перенос данных из плоскости в трехмерное пространство, где возможно построить такую плоскость, которая идеально разделит множество образцов на два класса. Опорными векторами в этом случае будут служить объекты из обоих классов, являющиеся экстремальными.
Таким образом, при помощи добавления так называемого оператора ядра и дополнительных размерностей, находятся границы между классами в виде гиперплоскостей.
Однако следует помнить: сложность построения SVM-модели заключается в том, что чем выше размерность пространства, тем сложнее с ним работать. Один из вариантов работы с данными высокой размерности - это предварительное применение какого-либо метода понижения размерности данных для выявления наиболее существенных компонент, а затем использование метода опорных векторов.
Как и любой другой метод, метод SVM имеет свои сильные и слабые стороны, которые следует учитывать при выборе данного метода.
Недостаток метода состоит в том, что для классификации используется не все множество образцов, а лишь их небольшая часть, которая находится на границах.
Достоинство метода состоит в том, что для классификации методом опорных векторов, в отличие от большинства других методов, достаточно небольшого набора данных. При правильной работе модели, построенной на тестовом множестве, вполне возможно применение данного метода на реальных данных.
Метод опорных векторов позволяет [37, 38]:
получить функцию классификации с минимальной верхней оценкой ожидаемого риска (уровня ошибки классификации);использовать линейный классификатор для работы с нелинейно разделяемыми данными, сочетая простоту с эффективностью.
Метод "ближайшего соседа" или системы рассуждений на основе аналогичных случаев
Следует сразу отметить, что метод "ближайшего соседа" ("nearest neighbour") относится к классу методов, работа которых основывается на хранении данных в памяти для сравнения с новыми элементами. При появлении новой записи для прогнозирования находятся отклонения между этой записью и подобными наборами данных, и наиболее подобная (или ближний сосед) идентифицируется.
Например, при рассмотрении нового клиента банка, его атрибуты сравниваются со всеми существующими клиентами данного банка (доход, возраст и т.д.). Множество "ближайших соседей" потенциального клиента банка выбирается на основании ближайшего значения дохода, возраста и т.д.
При таком подходе используется термин "k-ближайший сосед" ("k-nearest neighbour"). Термин означает, что выбирается k "верхних" (ближайших) соседей для их рассмотрения в качестве множества "ближайших соседей". Поскольку не всегда удобно хранить все данные, иногда хранится только множество "типичных" случаев. В таком случае используемый метод называют рассуждением по аналогии (Case Based Reasoning, CBR), рассуждением на основе аналогичных случаев, рассуждением по прецедентам.
Прецедент - это описание ситуации в сочетании с подробным указанием действий, предпринимаемых в данной ситуации.
Подход, основанный на прецедентах, условно можно поделить на следующие этапы:
сбор подробной информации о поставленной задаче;сопоставление этой информации с деталями прецедентов, хранящихся в базе, для выявления аналогичных случаев;выбор прецедента, наиболее близкого к текущей проблеме, из базы прецедентов;адаптация выбранного решения к текущей проблеме, если это необходимо;проверка корректности каждого вновь полученного решения;занесение детальной информации о новом прецеденте в базу прецедентов.Таким образом, вывод, основанный на прецедентах, представляет собой такой метод анализа данных, который делает заключения относительно данной ситуации по результатам поиска аналогий, хранящихся в базе прецедентов.
Данный метод по своей сути относится к категории "обучение без учителя", т.е. является "самообучающейся" технологией, благодаря чему рабочие характеристики каждой базы прецедентов с течением времени и накоплением примеров улучшаются. Разработка баз прецедентов по конкретной предметной области происходит на естественном для человека языке, следовательно, может быть выполнена наиболее опытными сотрудниками компании - экспертами или аналитиками, работающими в данной предметной области.
Однако это не означает, что CBR-системы самостоятельно могут принимать решения. Последнее всегда остается за человеком, данный метод лишь предлагает возможные варианты решения и указывает на самый "разумный" с ее точки зрения.
Метод опорных векторов
Метод опорных векторов (Support Vector Machine - SVM) относится к группе граничных методов. Она определяет классы при помощи границ областей.
При помощи данного метода решаются задачи бинарной классификации.
В основе метода лежит понятие плоскостей решений.
Плоскость (plane) решения разделяет объекты с разной классовой принадлежностью.
На рис.10.1 приведен пример, в котором участвуют объекты двух типов. Разделяющая линия задает границу, справа от которой - все объекты типа brown (коричневый), а слева - типа yellow (желтый). Новый объект, попадающий направо, классифицируется как объект класса brown или - как объект класса yellow, если он расположился по левую сторону от разделяющей прямой. В этом случае каждый объект характеризуется двумя измерениями.

Рис. 10.1. Разделение классов прямой линией
Цель метода опорных векторов - найти плоскость, разделяющую два множества объектов; такая плоскость показана на рис. 10.2. На этом рисунке множество образцов поделено на два класса: желтые объекты принадлежат классу А, коричневые - классу В.

Рис. 10.2. К определению опорных векторов
Метод отыскивает образцы, находящиеся на границах между двумя классами, т.е. опорные вектора; они изображены на рис. 10.3.
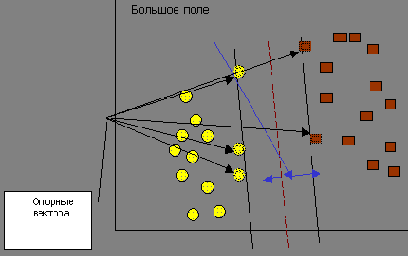
Рис. 10.3. Опорные векторы
Опорными векторами называются объекты множества, лежащие на границах областей.
Классификация считается хорошей, если область между границами пуста.
На рис. 10.3.показано пять векторов, которые являются опорными для данного множества.
Метод опорных векторов. Метод "ближайшего соседа". Байесовская классификация
В предыдущих лекциях мы рассмотрели такие методы классификации и прогнозирования как линейная регрессия и деревья решений; в этой лекции мы продолжим знакомство с методами этой группы и рассмотрим следующие из них: метод опорных векторов, метод ближайшего соседа (метод рассуждений на основе прецедентов) и байесовскую классификацию.
Недостатки метода "ближайшего соседа"
Данный метод не создает каких-либо моделей или правил, обобщающих предыдущий опыт, - в выборе решения они основываются на всем массиве доступных исторических данных, поэтому невозможно сказать, на каком основании строятся ответы.Существует сложность выбора меры "близости" (метрики). От этой меры главным образом зависит объем множества записей, которые нужно хранить в памяти для достижения удовлетворительной классификации или прогноза. Также существует высокая зависимость результатов классификации от выбранной метрики.При использовании метода возникает необходимость полного перебора обучающей выборки при распознавании, следствие этого - вычислительная трудоемкость. Типичные задачи данного метода - это задачи небольшой размерности по количеству классов и переменных.
С помощью данного метода решаются задачи классификации и регрессии.
Рассмотрим подробно принципы работы метода k-ближайших соседей для решения задач классификации и регрессии (прогнозирования).
Оценка параметра k методом кросс-проверки
Один из вариантов оценки параметра k - проведение кросс-проверки (Bishop, 1995).
Такая процедура реализована, например, в пакете STATISTICA (StatSoft) [39].
Кросс-проверка - известный метод получения оценок неизвестных параметров модели. Основная идея метода - разделение выборки данных на v "складок". V "складки" здесь суть случайным образом выделенные изолированные подвыборки.
По фиксированному значению k строится модель k-ближайших соседей для получения предсказаний на v-м сегменте (остальные сегменты при этом используются как примеры) и оценивается ошибка классификации. Для регрессионных задач наиболее часто в качестве оценки ошибки выступает сумма квадратов, а для классификационных задач удобней рассматривать точность (процент корректно классифицированных наблюдений).
Далее процесс последовательно повторяется для всех возможных вариантов выбора v. По исчерпании v "складок" (циклов), вычисленные ошибки усредняются и используются в качестве меры устойчивости модели (т.е. меры качества предсказания в точках запроса). Вышеописанные действия повторяются для различных k, и значение, соответствующее наименьшей ошибке (или наибольшей классификационной точности), принимается как оптимальное (оптимальное в смысле метода кросс-проверки).
Следует учитывать, что кросс-проверка - вычислительно емкая процедура, и необходимо предоставить время для работы алгоритма, особенно если объем выборки достаточно велик.
Второй вариант выбора значения параметра k - самостоятельно задать его значение. Однако этот способ следует использовать, если имеются обоснованные предположения относительно возможного значения параметра, например, предыдущие исследования сходных наборов данных.
Метод k-ближайших соседей показывает достаточно неплохие результаты в самых разнообразных задачах.
Примером реального использования описанного выше метода является программное обеспечение центра технической поддержки компании Dell, разработанное компанией Inference. Эта система помогает сотрудникам центра отвечать на большее число запросов, сразу предлагая ответы на распространенные вопросы и позволяя обращаться к базе во время разговора по телефону с пользователем. Сотрудники центра технической поддержки, благодаря реализации этого метода, могут отвечать одновременно на значительное число звонков. Программное обеспечение CBR сейчас развернуто в сети Intranet компании Dell.
Инструментов Data Mining, реализующих метод k-ближайших соседей и CBR-метод, не слишком много. Среди наиболее известных: CBR Express и Case Point (Inference Corp.), Apriori (Answer Systems), DP Umbrella (VYCOR Corp.), KATE tools (Acknosoft, Франция), Pattern Recognition Workbench (Unica, США), а также некоторые статистические пакеты, например, Statistica.
Преимущества метода
Простота использования полученных результатов.Решения не уникальны для конкретной ситуации, возможно их использование для других случаев.Целью поиска является не гарантированно верное решение, а лучшее из возможных.
Решение задачи классификации новых объектов
Эта задача схематично изображена на рис. 10.5. Примеры (известные экземпляры) отмечены знаком "+" или "-", определяющим принадлежность к соответствующему классу ("+" или "-"), а новый объект, который требуется классифицировать, обозначен красным кружочком. Новые объекты также называют точками запроса.
Наша цель заключается в оценке (классификации) отклика точек запроса с использованием специально выбранного числа их ближайших соседей. Другими словами, мы хотим узнать, к какому классу следует отнести точку запроса: как знак "+" или как знак "-".

Рис. 10.5. Классификация объектов множества при разном значении параметра k
Для начала рассмотрим результат работы метода k-ближайших соседей с использованием одного ближайшего соседа. В этом случае отклик точки запроса будет классифицирован как знак плюс, так как ближайшая соседняя точка имеет знак плюс.
Теперь увеличим число используемых ближайших соседей до двух. На этот раз метод k-ближайших соседей не сможет классифицировать отклик точки запроса, поскольку вторая ближайшая точка имеет знак минус и оба знака равноценны (т.е. победа с одинаковым количеством голосов).
Далее увеличим число используемых ближайших соседей до 5. Таким образом, будет определена целая окрестность точки запроса (на графике ее граница отмечена красной( серой) окружностью). Так как в области содержится 2 точки со знаком "+" и 3 точки со знаком "-" , алгоритм k-ближайших соседей присвоит знак "-" отклику точки запроса.
Решение задачи прогнозирования
Далее рассмотрим принцип работы метода k-ближайших соседей для решения задачи регрессии. Регрессионные задачи связаны с прогнозированием значения зависимой переменной по значениям независимых переменных набора данных.
Рассмотрим график, показанный на рис. 10.6. Изображенный на ней набор точек (зеленые прямоугольники) получен по связи между независимой переменной x и зависимой переменной y (кривая красного цвета). Задан набор зеленых объектов (т.е. набор примеров); мы используем метод k-ближайших соседей для предсказания выхода точки запроса X по данному набору примеров (зеленые прямоугольники).
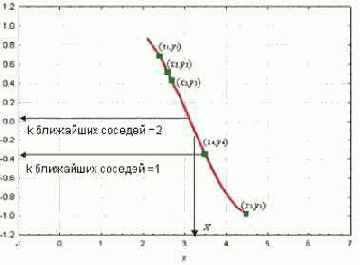
Рис. 10.6. Решение задачи прогнозирования при разных значениях параметра k
Сначала рассмотрим в качестве примера метод k-ближайших соседей с использованием одного ближайшего соседа, т.е. при k, равном единице. Мы ищем набор примеров (зеленые прямоугольники) и выделяем из их числа ближайший к точке запроса X. Для нашего случая ближайший пример - точка (x4 ;y4). Выход x4 (т.е. y4), таким образом, принимается в качестве результата предсказания выхода X (т.е. Y). Следовательно, для одного ближайшего соседа можем записать: выход Y равен y4 (Y = y4 ).
Далее рассмотрим ситуацию, когда k равно двум, т.е. рассмотрим двух ближайших соседей. В этом случае мы выделяем уже две ближайшие к X точки. На нашем графике это точки y3 и y4 соответственно. Вычислив среднее их выходов, записываем решение для Y в виде Y = (y3 + y4)/2.
Решение задачи прогнозирования осуществляется путем переноса описанных выше действий на использование произвольного числа ближайших соседей таким образом, что выход Y точки запроса X вычисляется как среднеарифметическое значение выходов k-ближайших соседей точки запроса.
Независимые и зависимые переменные набора данных могут быть как непрерывными, так и категориальными. Для непрерывных зависимых переменных задача рассматривается как задача прогнозирования, для дискретных переменных - как задача классификации.
Предсказание в задаче прогнозирования получается усреднением выходов k-ближайших соседей, а решение задачи классификации основано на принципе "по большинству голосов".
Критическим моментом в использовании метода k-ближайших соседей является выбор параметра k. Он один из наиболее важных факторов, определяющих качество прогнозной либо классификационной модели.
Если выбрано слишком маленькое значение параметра k, возникает вероятность большого разброса значений прогноза. Если выбранное значение слишком велико, это может привести к сильной смещенности модели. Таким образом, мы видим, что должно быть выбрано оптимальное значение параметра k. То есть это значение должно быть настолько большим, чтобы свести к минимуму вероятность неверной классификации, и одновременно, достаточно малым, чтобы k соседей были расположены достаточно близко к точке запроса.
Таким образом, мы рассматриваем k как сглаживающий параметр, для которого должен быть найден компромисс между силой размаха (разброса) модели и ее смещенностью.
